Finding Match Sets
- Author:
- Serge Monkewitz
| Contents | |
Lane Subdivision
The problem of finding a match set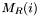 for an apparition
for an apparition 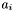 is made efficient by limiting the number of apparitions which are tested for membership.
is made efficient by limiting the number of apparitions which are tested for membership.
The specific approach taken by the WAX software is to assign apparitions to small lanes (spatial bins corresponding to a range of declinations and right ascensions), and then determining, given a lane 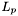 , which other lanes contain apparitions that potentially belong to match sets of apparitions in
, which other lanes contain apparitions that potentially belong to match sets of apparitions in 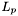 . For any single apparition, only a tiny area of the sky is examined to find a match set. This is the key to obtaining good performance in the swiss cheese algorithm.
. For any single apparition, only a tiny area of the sky is examined to find a match set. This is the key to obtaining good performance in the swiss cheese algorithm.
Specifically, each band 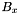 is split into lanes
is split into lanes 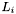 where
where 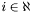 ,
, 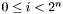 and
and 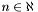 ,
, 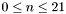 . Each lane covers a range of right ascensions :
. Each lane covers a range of right ascensions :
-
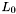 covers right ascensions in the range
covers right ascensions in the range 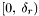
-
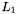 covers right ascensions in the range
covers right ascensions in the range 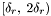
- ...
-
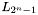 covers right ascensions in the range
covers right ascensions in the range 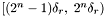
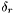 is equal to
is equal to 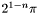 radians.
radians. Determining the number of lanes per band
The actual number of lanes in a band is determined by picking a minimum lane width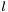 , defined to be the smallest distance between a position
, defined to be the smallest distance between a position 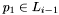 and
and 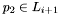 .
.
Without loss of generality, let 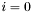 (the angle between unit vectors is invariant under rotation). Furthermore, define
(the angle between unit vectors is invariant under rotation). Furthermore, define 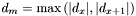 . This minimum distance occurs between the positions
. This minimum distance occurs between the positions 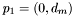 and
and 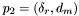 , expressed in polar coordinates (unless
, expressed in polar coordinates (unless 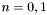 , in which case this minimum distance is either undefined or zero).
, in which case this minimum distance is either undefined or zero).
When expressed as vectors in 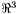 ,
, 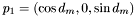 and
and 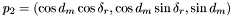 . Using the relation
. Using the relation 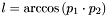 , the following formula is obtained :
, the following formula is obtained :
![\[ \cos{l} = \cos^2{d_m}\cos{\delta_r} + \sin^2{d_m} \]](form_38.png)
To find the number of lanes in a band the actual lane width for each possible value of 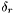 is computed. The number of lanes is determined from the largest
is computed. The number of lanes is determined from the largest 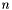 resulting in a lane width greater than the requested minimum, or
resulting in a lane width greater than the requested minimum, or 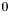 if this is impossible. For example, bands containing a pole have a lane width of zero regardless of
if this is impossible. For example, bands containing a pole have a lane width of zero regardless of 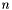 and will therefore contain just a single lane. Since this directly effects the efficiency of the match set finding algorithm, the pole bands should be as skinny as possible.
and will therefore contain just a single lane. Since this directly effects the efficiency of the match set finding algorithm, the pole bands should be as skinny as possible.
The WAX application uses a minimum lane width of 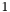 arcsecond when the -o option is specified, and
arcsecond when the -o option is specified, and 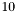 arcseconds otherwise.
arcseconds otherwise.
Mapping positions (apparitions) to lanes
Positions are trivially mapped to lanes: given a right ascension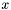 for a position, the enclosing lane
for a position, the enclosing lane 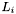 is determined as follows :
is determined as follows :
![\[ i = \lfloor x\delta_r^{-1} \rfloor \]](form_44.png)
Once all apparitions in a band have been retrieved and assigned to the appropriate lanes, the apparitions in each lane are sorted in order of increasing declination.
Finding lane windows
Given an arbitrary apparition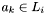 , define the lane window
, define the lane window 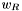 to be the number of lanes
to be the number of lanes 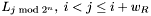 which can contain an apparition falling into the match set
which can contain an apparition falling into the match set 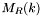 . Due to rotational symmetry,
. Due to rotational symmetry, 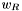 will be identical for all lanes in a band.
will be identical for all lanes in a band.
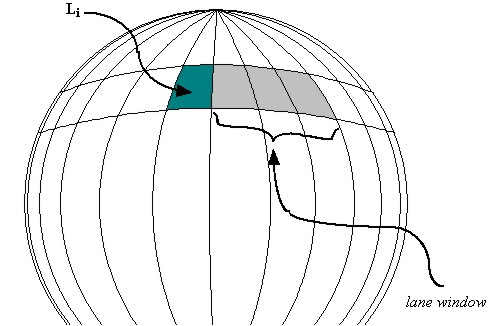
Using the relations derived above, the lane window is the smallest integer 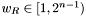 satisfying
satisfying
![\[ \cos{R} > \cos^2{d_m}\cos{w_R\delta_r} + \sin^2{d_m} \]](form_50.png)
or 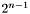 if the relation cannot be satisfied.
if the relation cannot be satisfied.
Finding a match set
To find a match set for an apparition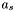 with position
with position 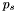 , given a lane window
, given a lane window 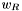 and a search radius
and a search radius 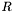 , first find the lane
, first find the lane 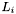 enclosing
enclosing 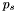 . To find all apparitions in the match set
. To find all apparitions in the match set 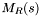 , it is sufficient to consider apparitions in lanes
, it is sufficient to consider apparitions in lanes 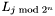 where
where 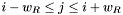 if
if 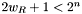 , or
, or 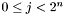 otherwise.
otherwise.
Furthermore, if the position 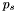 has a declination
has a declination 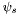 , then apparitions in the match set
, then apparitions in the match set 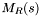 will have declinations in the range
will have declinations in the range ![$[\psi_s - R,\; \psi_s + R]$](form_61.png) . For each
. For each 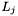 being searched, the apparitions in this range can be found using a simple binary search (since apparitions within a lane are declination sorted). Each such apparition
being searched, the apparitions in this range can be found using a simple binary search (since apparitions within a lane are declination sorted). Each such apparition 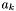 is then tested against
is then tested against 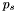 , and included in
, and included in 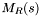 if and only if
if and only if
![\[ \cos{R} \leq p_s \cdot p_k \]](form_64.png)
Lane Walks
The density pass and swiss cheese pass of the swiss cheese algorithm involve computing match sets for almost all retrieved apparitions and allow freedom in the order in which match sets are found.Number the apparitions based on their enclosing lane and position within that lane as follows :
![\[ L_i = \{ a_{i0}, a_{i1}, a_{i2}, \ldots \} \]](form_65.png)
where 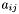 has declination
has declination 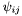 . Since the apparitions in a lane are declination sorted,
. Since the apparitions in a lane are declination sorted,
![\[ v > u \Leftrightarrow \psi_{iv} \geq \psi_{iu} \]](form_68.png)
By "walking" up the apparitions within a single lane 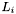 , finding match sets for
, finding match sets for 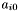 , then
, then 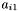 , etc... the match set finding process can be made even more efficient :
, etc... the match set finding process can be made even more efficient :
-
The lanes
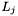 containing potential members of a match set for
containing potential members of a match set for 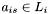 need only be computed once
need only be computed once 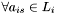 .
. -
The range of apparitions
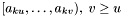 within declination
within declination 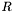 of
of 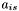 can be used as a starting point for finding the range of apparitions within declination
can be used as a starting point for finding the range of apparitions within declination 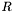 of
of 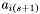 .
.
This leads to the lane walking algorithm described below.
Finding matches from a single lane
Let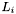 be the lane containing apparitions for which match sets are desired. Let
be the lane containing apparitions for which match sets are desired. Let 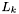 be one of the lanes potentially containing matches for these apparitions.
be one of the lanes potentially containing matches for these apparitions.
Consider the first apparition 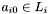 . Find the smallest non-negative integer
. Find the smallest non-negative integer 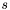 such that
such that 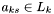 has declination
has declination 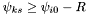 (using a binary or linear search).
(using a binary or linear search).
Now, let 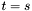 . While
. While 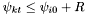 :
:
-
add
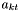 to the match set for
to the match set for 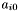 if and only if
if and only if 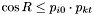
-
increment

At this point, all apparitions in 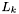 belonging to the match set for
belonging to the match set for 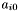 have been found, so the next apparition in
have been found, so the next apparition in 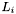 ,
, 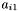 is considered. To find the first apparition in
is considered. To find the first apparition in 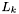 possibly belonging to the match set for
possibly belonging to the match set for 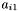 , increment
, increment 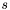 until
until 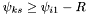 . Then repeat the steps above, finding all apparitions in
. Then repeat the steps above, finding all apparitions in 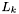 belonging to the match set for
belonging to the match set for 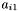 .
.
Continue in similar fashion until all apparitions in 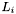 have been considered.
have been considered.
Final match set finding algorithm
The final algorithm for match set finding simply repeats the steps detailed above for each lane potentially containing matches for apparitions in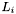 (these are determined using the lane window
(these are determined using the lane window 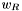 ).
).
By walking each lane 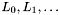 in this manner, match sets for every apparition in
in this manner, match sets for every apparition in 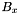 are found.
are found.
Generated on Thu Oct 21 13:19:38 2004 for WAX Version 2.1 by